SOMOS DE MATILLAS: FRACCIONES

Otras viejas conocidas. Vamos, que no tienes excusa para bordar este tema.

Ya sabemos que podemos expresar las cantidades de formas muy variadas. Las fracciones son una de esas formas.

Te voy a contar una historia:

El día del cumple de la hermana de Samara su mamá había preparado una deliciosa tarta de chocolate, precisamente la preferida de Samara.
Cuando llegó la hora de la fiesta, mamá salió de la cocina enfadadísima, fue directa a Samara y la riñó mucho, muchísimo.
Samara se disculpaba diciendo que él sólo había comido una fracción de la tarta, para ser exactos 8/8, no era para tanto... ¿o sí...?

¿Crees que el enfado de la mamá de Samara está justificado?

CONCEPTO DE FRACCIÓN

Una fracción expresa un cociente, una división entre dos números. El de abajo, que se llama denominador, me dice en cuántas partes está dividida la unidad. El de arriba, el numerador, lo que me cuenta es cuántas partes estoy cogiendo. Por lo tanto, cuando el numerador y el denominador son iguales lo que significa es que cojo todas las partes en que está dividida la unidad, es decir, lo cojo todo.

De esta forma, una fracción puede representar cantidades iguales a la unidad, cuando numerador y denominador son iguales, cantidades menores que la unidad, cuando el numerador es más pequeño que el denominador, y cantidades mayores que la unidad, cuando el numerador es mayor que el denominador, eso significa que me he comido una parte entera y una fracción de otra.

Vamos a ponerlo en práctica, puedes ejercitarte a continuación:
Este enlace es genial para empezar. Tienes explicaciones y actividades para todo el tema.

También este es muy completo y divertido:

$Números_fraccionarios$

Y otro más:

$Ejercicios_de_fracciones$

COMPARAMOS FRACCIONES
OTRO POCO

¡QUÉ FÁAACILLLL!

Si quieres ir poco a poco, mira a continuación.
FRACCIONES EQUIVALENTES
Vamos a probar tus dotes deductivas. ¿qué significa eso de equivalentes?, ya sabes que el prefijo "equi-" significa igual, y ¿qué puede significar "-valente"? Eso es, equivalentes significa de igual valor, es decir, son formas distintas de expresar una misma cantidad.

1	=	2	=	4

2		4		8

Y en un dibujo se ve así:

1/2		2/4		4/8
	=		=

Si te fijas, lo que estamos haciendo es multiplicar el numerador y el denominador pro el mismo número, de este modo la fracción mantiene su valor, es decir, sigue representando la misma cantidad de pizza. La regla a recordar es:

¡Lo que haces a la parte de arriba de la fracción también lo tienes que hacer a la parte de abajo!

Por eso, estas fracciones son en realidad la misma:

	× 2		× 2

1	=	2	=	4

2		4		8

	× 2		× 2

También puedo lograr fracciones equivalentes dividiendo, en vez de multiplicando, el numerador y el denominador por el mismo número.

	÷ 3		÷ 6

18	=	6	=	1

36		12		2

	÷ 3		÷ 6

Lo único que debes de tener en cuenta es que cuando lo que hago es dividir tengo que buscar un número que sea divisor a la vez del número que está en el numerador y del número que está en el denominador, la división tiene que se exacta, por lo tanto tengo que buscar divisores comunes. Recuerda el tema de la divisibilidad.

Cuando busco fracciones equivalentes a una dada por este método de dividir los dos términos de la fracción lo que consigo son fracciones cada vez más pequeñas, las estoy reduciendo o simplificando, hasta llegar a un punto en que ya no puede ser más pequeña, esa fracción se llama IRREDUCIBLE.

Para ver más cosas:

FRACCIONES EQUIVALENTES
LIBROS VIVIOS SM
ANAYA
FRACCIONES IRREDUCIBLES

Las fracciones equivalentes nos pueden resultar muy útiles.
Cuando comparamos fracciones la tarea puede ser muy sencilla: si tenemos el mismo denominador la fracción más grande es la que tiene el numerador mayor, en el caso de que tengan el mismo numerador la fracción más grande es la que tiene el denominador más pequeño (los trozos son más grandes, luego representa mayor cantidad).

$Resultado de imagen de comparar fracciones 5º primaria$

COMPARAR FRACCIONES

SANTILLANA

Pero también puede ser muy complicada, cuando tenemos que comparar fracciones de distintos denominadores y distintos numeradores. ¿Qué hacemos entonces?
Aquí es donde intervienen las fracciones equivalentes.
Se trata de cambiar las fracciones que me dan por otras que valgan lo mismo pero con las que me resulte más fácil trabajar, es decir, voy a buscar fracciones equivalentes a las que me dan con un denominador igual, esto es lo que se llama COMÚN DENOMINADOR
Aquí tienes un enlace que te enseña a reducir a común denominador.

OPERACIONES CON FRACCIONES

FRACCIÓN DE UN NÚMERO Como ya hemos dicho una fracción expresa una cantidad determinada, no es más que una división. En ocasiones las fracciones vienen relacionadas con un número, es decir, lo que tengo que averiguar es la fracción de un determinado número. Por ejemplo, si he realizado los 3/5 de los 20 ejercicios de matemáticas, eso quiere decir que he hecho 12 ejercicios. Te adjunto un enlace donde lo explica muy bien, espero que lo comprendas.

FRACCIÓN DE UN NÚMERO
AHORA PRACTICA UN POCO MÁS

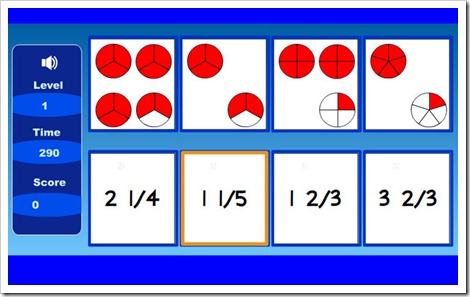
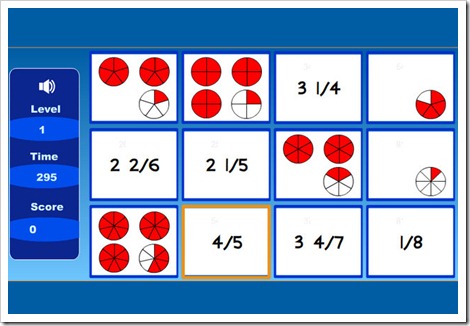
NÚMEROS MIXTOS

Mira estas fracciones: 13/4; 17/5; 9/2

Si te das cuenta, aunque el numerador es mayor que el denominador, no equivalen a un número natural; es decir, la división entre el numerador y el denominador no es exacta. Sin embargo, también las puedo expresar de otra manera: son los NÚMEROS MIXTOS, formados por un número natural seguido de una fracción.

¿Qué significa que he comprado 13/4 de empanada?

1.- Que las empanadas están divididas en 4 porciones.

2.- Que he comprado 13 porciones.

3.- Por tanto eso equivale a 3 empanadas enteras -12/4- más 1/4 de otra empanada.

4.- Eso se representa con un número mixto:3 ¼

Puedes mirar aquí para saber más sobre los números mixtos:

NÚMEROS MIXTOS EXPLICACIÓN

Bueno, vamos a resumir un poco todo esto de los números mixtos.
Cosas que debes recordar:
1.- Una fracción es una división, el numerador es el dividendo y el denominador es el divisor.
2.- Las fracciones representan cantidades. Pueden ser más pequeñas que la unidad -cuando el numerador es más pequeño que el denominador; iguales que la unidad - cuando numerador y denominador son iguales; o mayores que la unidad -cuando el numerador es mayor que el denominador.
3.- El Las fracciones mayores que la unidad, hay veces que la división del numerador entre el denominador me da un número exacto. Eso significa que he tomado lo que sea que esté representado de forma total: 12/3 de tortilla= 4 tortillas enteras; 15/5 de tortilla= 3 tortillas enteras...
Cuando la división no da exacta significa que, además de las enteras también he tomado una parte de otra, la que indica el resto.

Ejemplos:

Un número mixto está formado por un número natural y una fracción. Todas las fracciones mayores que la unidad se pueden expresar en forma de número mixto.

Hay dos casos:

Primero. Pasar de fracción a número mixto. Ejemplo 8/5. Se hace la división 8:5= 1 y el resto es 3. Por tanto: 1 es el número natural y 3 es el numerador de la fracción y le denominador no cambia, es decir 5.

Segundo: Pasar de número mixto a fracción. El numero natural se multiplica por el denominador y se suma el numerador. Ejemplo 1 + 2/3. Operamos: 1 x 3 = 3+2 = 5